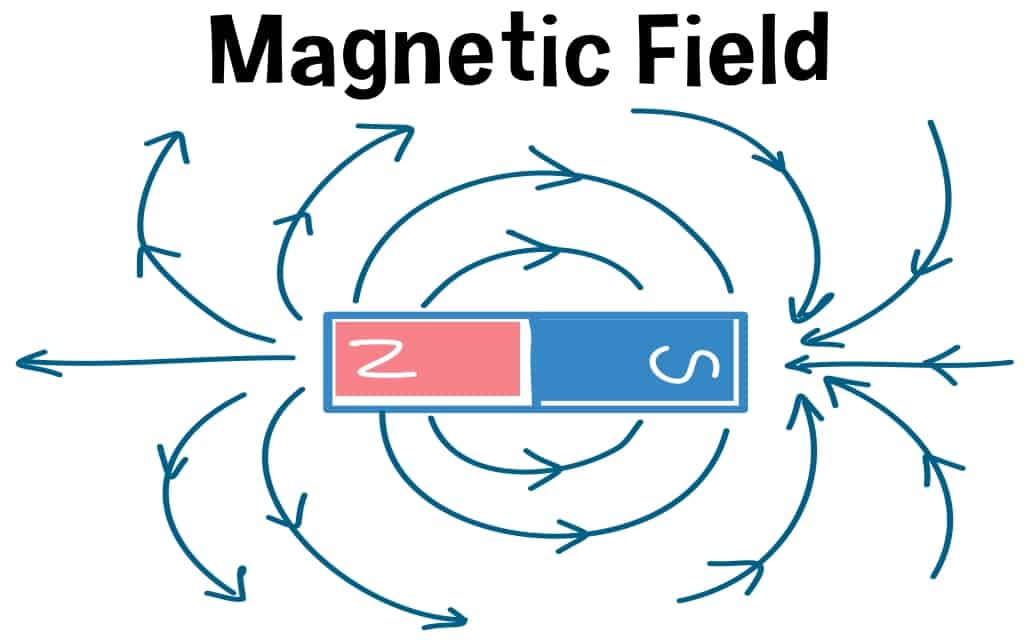
Magnet is a unique substance that has the property to attract materials which exhibit magnetic properties. A magnetic field is created irrespective of the size of the magnet. Let us understand and learn the magnetic field definition along with its behavior.
In simple words, the magnetic field is defined as the area around the magnet which experiences the magnetic force. The magnetic field is a vector field created in the vicinity of electric current, a magnet, or changing electric field, in which magnetic forces are noticed.
As we know, a magnet has two poles and the attraction or repulsion is determined by the orientation of the magnets. The magnetic field is described mathematically as a vector field, where each vector points in the direction of a compass. The magnetic induction or magnetic flux density is represented by B. The magnetic field intensity or magnetic field strength is represented by letter H.
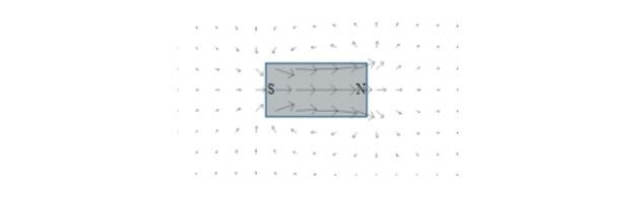
Magnetic lines of force is an alternate way to represent the magnetic lines of force around the magnet. Magnetic lines of force are as shown in the figure below.
Know some of the facts about magnetic lines
- Magnetic field lines never cross
- Magnetic field lines always make a closed loop, means it starts at one end and terminates at another end passing through the magnet.
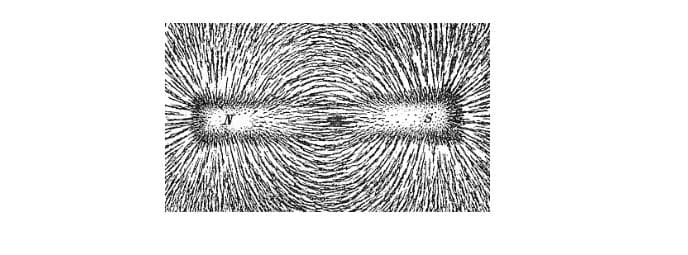
We can witness magnetic lines of force using a simple way.
Magnetic field lines can be seen near the magnet or magnetic material by dropping some amount of iron filings near the magnet. Each filing spread near the magnet behaves like a little magnet with a north and south pole. Since the same poles repel and opposite poles attract each other. The filings separate from each other because similar poles repel each other. The result in the pattern that resembles magnetic field lines. The magnetic lines in the magnetic field are as shown in the figure below:
Displacement Current
We know that the magnetic field is associated with an electric current. Displacement current is defined as the rate of change (displacement) of the electric field (D).
Hence,
i = ic + id
= ic + ε0(dQ/dt)
Where,
ic = conduction current
id = displacement current
According to Maxwell’s equation, Displacement current has the same unit and effect on the magnetic field as is for conduction current.
In a capacitor, there is no conduction of charge between the plates when it starts charging. However, because of the change in charge accumulation with time above the plates, the electric field changes witnesses the displacement current. It is given by
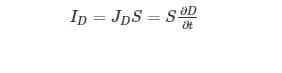
Where,
- S = area of the capacitor plate.
- ID = displacement current.
- JD = displacement current density.
- D = related to electric field E as D=εE
- ε = permittivity of the medium in between the plates.
Displacement Current Equation
According to Maxwell’s equation for conduction current, displacement current has the same unit and effect on the magnetic field –
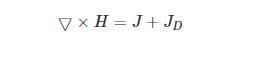
Where,
- H = related to magnetic field B as B=μH
- μ = permeability of the medium in between the plates.
- J is the conducting current density.
- JD is the displacement current density.
To know more about the magnetic field and displacement current, visit BYJU’S.